ピタゴラスの定理 大矢真一著 参考 図1の大きな正方形は右のように組みかえると、図2のような二つの正方形およびの和となる。 これを代数的に考えると、図1で よって、二辺とその間の角が、それぞれ等しいため 同様にすると 四つの直角三角形は合同である。 ゆえに c²=2ab+(b-a)²No027 ピタゴラスと直角三角形 「ピタゴラスの定理」を知っていますか? これは「直角三角形の斜辺上に立つ正方形の面積は、他の2辺上に立つ正方形の面積の和に等しい」 という定理です。 これはどういうことか? では、図を使って説明します。 三平方の定理にはたくさんの証明方法があります。今回は外接円と直角二等辺三角形を利用した証明方法について紹介します。 Ⅰ 三平方の定理とは 三平方の定理とは、次のような定理です。 三平方の定理(ピ

三平方の定理の証明と使い方
ピタゴラスの定理 直角三角形
ピタゴラスの定理 直角三角形-2 特殊な形の三角形で利用される三平方の定理 21 直角二等辺三角形:角度が45°の直角三角形;もくじ 1 三平方の定理の内容:直角三角形と辺の長さの関係 11 分からない辺の長さを計算できる三平方の定理;




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく
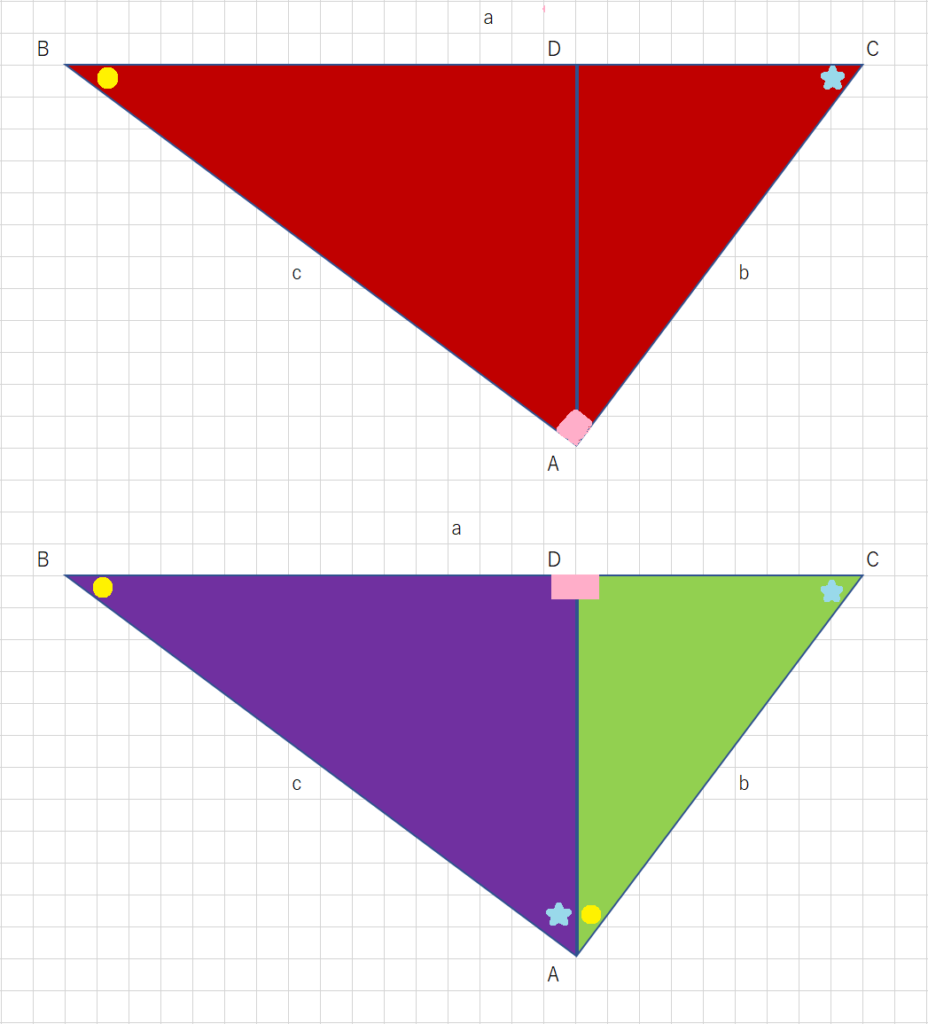
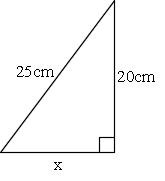
ピタゴラスの定理 「直角三角形で直角をはさむ2辺を、a、b、斜辺をcとした場合、a 2 b 2 =c 2 」という文章を図にすると、上のようになります。 なんとなく思い出しましたか? 2つの辺の長さが分かればもう一つの辺の長さが分かるという公式です。 この定理の証明方法は、数学的で複 つぎの直角三角形の辺の長さxを求めてください。 三平方の定理で直角三角形の辺の長さを計算してみると、 x² = 3² 5² x = √34 になるね。 答えが整数じゃなくてスッキリしないけど、こういう答えもありだ。 Step3 ピタゴラスが悩んだ直角二等辺三角直角三角形でない三角形の辺の長さは余弦定理で計算できます。本質問が「ピタゴラスの定理がどう使えるのか」ということなのでピタゴラスの定理を使って回答します。 三角形 math{\rm ABC}/math を考えます。各頂点に向かい合う変の長さを matha/math, mathb/math, mathc/math 三角形の辺 math{\rm BC}/math と math{\rm CA}/math が角度 math\theta/math
三平方の定理は、直角三角形の斜辺の2乗が他の辺の2乗の和に等しい、という公式です。 非常に便利ですが、二次方程式になってしまうので解答するのに時間がかかります。 そこで、テストによく出てくる直角三角形については暗記してしまいましょう。 ここでは、特に重要な7つのパ 3:4:5の三角形で,本当に直角ができるのでしょうか。 三角形の辺の長さの比と角の大きさには,どんな関係があるのでしょうか。 3:4:5は,斜辺の対角が直角です。このことは,三平方の定理として知られています。 3:4:5 三平方の定理(ピタゴラスの定理) 上のような直角三角形で、次の等式が成り立つ。 a2 b2 = c2 a 2 b 2 = c 2 直角三角形の2辺がわかれば、残りの1辺も求まるというもので、紀元前から測量等でも使われてきました。 日本では中学3年生(義務教育! )で
直角三角形の辺を $a,\ b,\ c$ (斜辺が $c$ )としたとき \ c^2=a^2b^2 \ を三平方の定理(ピタゴラスの定理)という。直角三角形に関する定理で、斜辺の二乗が残りの辺の二乗の和に等しい。 三平 ピタゴラスの定理を使って、良い比率の三角形を無限に生み出す 数学 Tweet Pocket ピタゴラスの定理(または三平方の定理)は、誰もが小学生や中学生の頃から知っている馴染み深い定理だろう。 ピタゴラスの定理を使って「3対4対5」など三辺の定理 直角三角形で、斜辺を直径とする半円が内接していて他の2辺を直径とする半円は外接している。 斜辺でない方の2辺の半円と直角三角形の和と斜辺の半円の面積の差は、元の直角三角形の面積と等しい。 つまり図では青と赤の面積が等しい。



三平方の定理



中学数学の最後にして最大の壁 三平方の定理はこれで満点ゲット 高校入試徹底対策ガイド
ピタゴラスの定理の逆 三角形 の三 ピタゴラスが,直角三角形 において「辺の長さの比」と「辺の長さに依存する正方形の面積」との関係,数(数式)と図形の関係に着目して定理を見出してることが興味深いところです。 図形を考察する際は,図形の「形」と「量」に着目することが必要 でもこれは、裏を返せば、「 直角三角形が出てきたら、三平方の定理(ピタゴラスの定理)を使えないかとりあえず考えてみないとダメ 」ということになりませんか? そんでもって、直角三角形ってメチャクチャ出てきますよね。 つまり、三平方の定理(ピタゴラスの定理)はメチャク三平方の定理(ピタゴラスの定理) ∠ACB=90°となる直角三角形ABCにおいて,各辺の長さを, BC = a , CA = b , AB = c とすると, a 2 b 2 = c 2 の関係が成り立つ.この関係を 三平方の定理 あるいは ピタゴラスの定理 という. 証明




数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース



三平方の定理を直角三角形以外の三角形に使う時の公式ってどうなりますか Yahoo 知恵袋
A 2 b 2 = c 2 ⊿ 直角三角形で、それぞれの辺の長さを 2 乗した正方形を考えます。 その三つの正方形の面積の関係性を語ったのが《三平方》の定理です。 底辺 2 + 高さ 2 = 斜ピタゴラス数とは,直角三角形の3辺の長さとなるような3つの整数の組のことです。 ピタゴラスの定理(三平方の定理)を使うと, a 2 b 2 = c 2 a^2b^2=c^2 a 2 b 2 = c 2 を満たす自然数の組 ( a , b , c ) (a,b,c) ( a , b , c ) をピタゴラス数と呼ぶ。直角三角形の直角を挟んだ2辺の長さをaとb、直角に対する斜辺 (もっとも長い辺)の長さをcとすると (図Math001)、つぎの等式が成立ちます。 これを「三平方の定理」あるいは「ピタゴラスの定理」と呼びます。 三平方の定理 a 2 b 2 = c 2 図Math001




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導
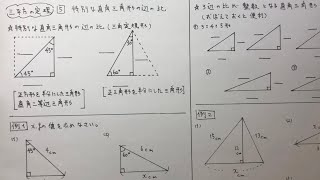



中3数学 三平方の定理5 特別な直角三角形の辺の比 すべて無料 星組の中学数学講座
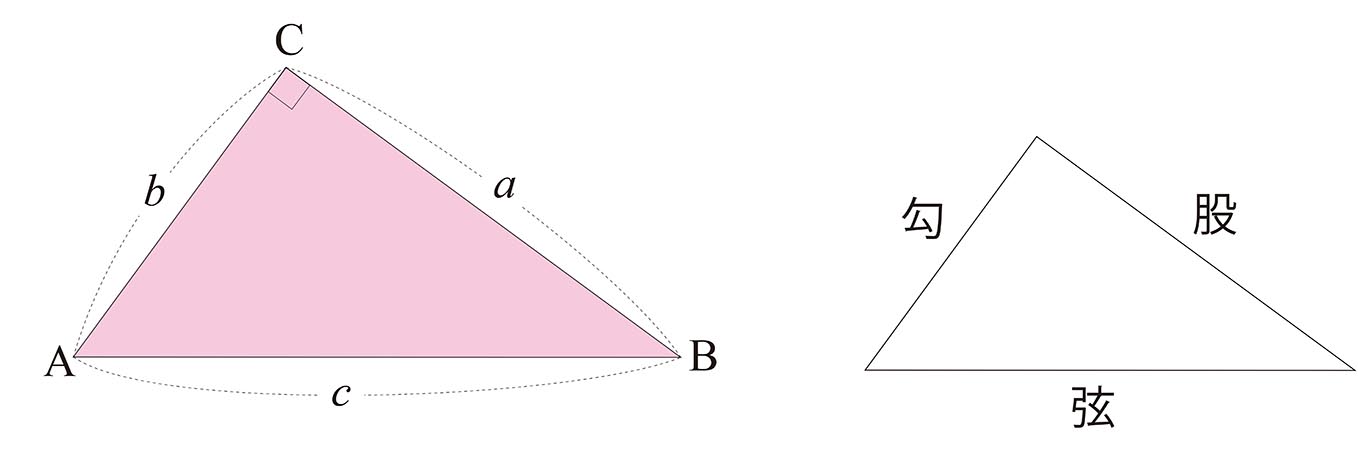
初等幾何学におけるピタゴラスの定理(ピタゴラスのていり、英 Pythagorean theorem )は、直角三角形の3辺の長さの関係を表す。 斜辺の長さを c, 他の2辺の長さを a, b とすると、定理は mathc^2=a^2b^2/math が成り立つという等式の形で述べられる 。 三平方の定理(さんへいほうのていり)、勾股弦ABCを直角三角形としてみましょう。 そうすると、二つの三角形は合同になり、ピタゴラスの定理がいえます。 これは、中点定理をより視覚的にしたものです。 三角形と正方形の作る三角形の間に不思議な関係が浮かび上がります。三平方の定理の証明5選直角三角形や正方形を重ねましょう 三平方の定理(別名ピタゴラスの定理)とは、底辺が $a$、高さが $b$、斜辺が $c$ である直角三角形において、$$a^2b^2=c^2$$ が成り立つことでしたね。




三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生
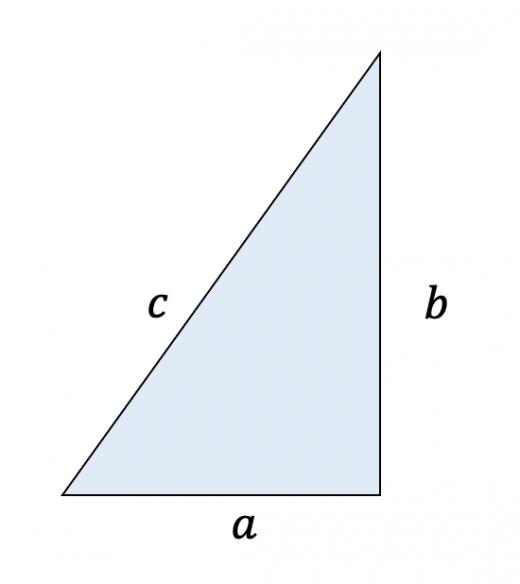
1.どんな定理か理解しよう! 三平方の定理はピタゴラスの定理、 勾股弦 こうこげん の定理とも呼びます。 この定理は、直角三角形の3つの辺の長さの関係を表しています。 上図の直角三角形では、直角を挟む2つの辺の長さがa、bで、斜辺の長さがcとなっています。直角三角形の直角をはさむ 2 辺の長さを a, b 、 斜辺 の長さを c とすると、 a 2 b 2 = c 2 (短い辺を 2 乗して足すと斜辺の 2 乗になる) ピタゴラスの定理とは 直角三角形の底辺の2乗と対辺の2乗をたすと斜辺の2乗に等しいというものです。 図で説明すると 数式をならべてもわかりにくいから絵とみくらべてください。



円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト
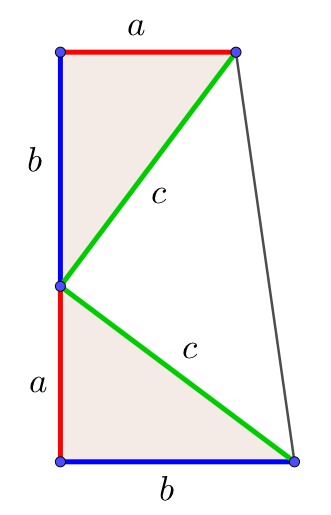



三平方の定理の証明3 大統領の台形 キソカラ
直角三角形において,斜辺の長さを $c$,他の $2$ 辺の長さを $a$, $b$ とすると $a^2b^2$ = $c^2$ が成り立つ.ご存知三平方の定理,いわゆるピタゴラスの定理だ. 江戸時代,日本では勾股弦(こう こ げん)の定理と呼ばれていた.三平方の定理(ピタゴラスの定理) 直角三角形において, a 2 b 2 = c 2 a^2b^2=c^2 a2 b2 = c2 つまり「斜辺以外の二辺の長さの二乗の和」は「斜辺の二乗」と等しい。 a, b, c a,b,c a,b,c は直角三角形の3辺の長さで, c c c が斜辺です。直角三角形abcでピタゴラス(三平方)の定理: 2 +1/b 2 =1/h 2
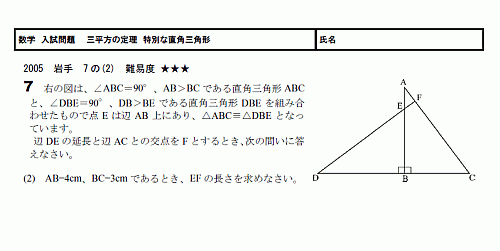



三平方の定理 スタディーx




3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく
です。これは直角二等辺三角形の場合の三平方の定理ですね! やはり、ピタゴラスは只者ではありません。 ちなみに、上のタイルを一般の直角三角形に応用した図は です。ここで面積が 大きな正方形=小さな正方形+直角三角形×4やさしいピタゴラスの定理(三平方の定理)の証明 を証明すれば十分な証明になります。 そのため、斜辺の長さが1の直角三角形を、斜辺に垂直な線(点線)で2つに分けると簡単に証明できる。 2つに分けられた線の長さはd2とe2。 問題の図形を斜辺に直角三角形の3辺の長さに関する a 2 b 2 =c 2 という関係は ピタゴラスの定理 (三平方の定理)と呼ばれます。 この定理はその名の通り古くから知られていますが、本当にピタゴラス (cBC570cBC500)が発見したかどうか確証があるわけではありません。




三平方の定理で辺を求める Youtube




三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題
ピタゴラスの定理(ピタゴラスのていり)は、 直角三角形 の3 辺 の長さの関係を表す 等式 である。三平方の定理(さんへいほうのていり)、勾股弦の定理(こうこげんのていり)とも呼ばれる。




三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト
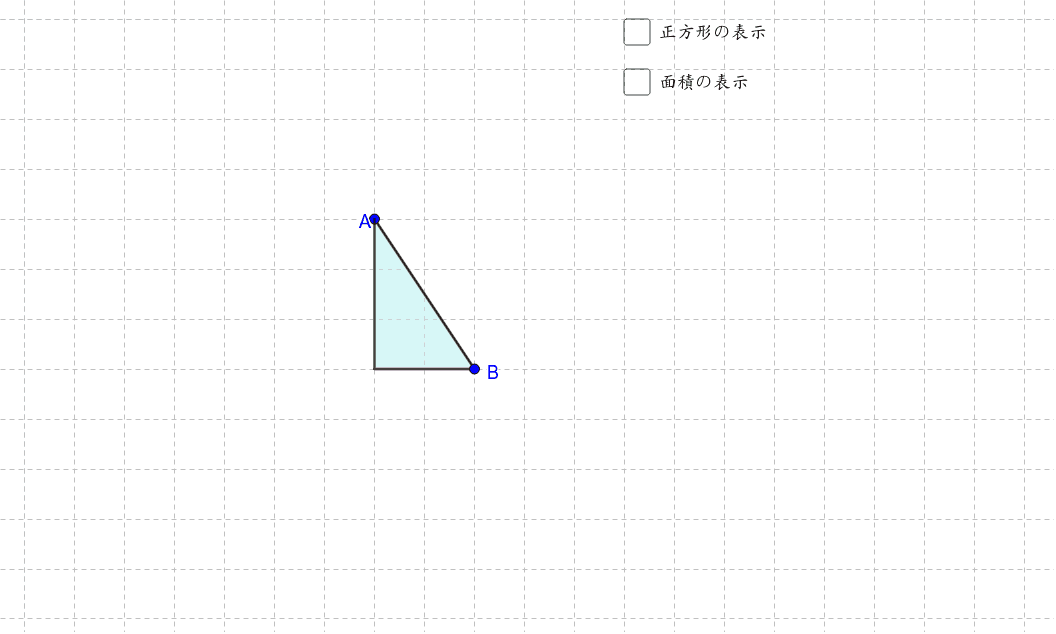



三平方の定理の導入 Geogebra




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




三平方の定理 ピタゴラスの定理 中学数学 By Okボーイ マナペディア




数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース



1




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ




中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su




特別な直角三角形の辺の比 無料で使える中学学習プリント




三平方の定理 おやじさん ネット




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく



中学数学 直角三角形の三平方の定理とは ピタゴラス 平方根 の定理をexcelの図形で Curlpingの幸せblog




三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ




中3数学 図でよくわかる三平方の定理 ピタゴラスの定理 の証明と計算問題 Irohabook




三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく




三平方の定理 特別な直角三角形の3辺の比 中学生からの勉強質問 数学 進研ゼミ中学講座




三平方の定理 覚えること 辺の長さ 苦手な数学を簡単に




無料 中3数学 基本解説 解答プリント 334 三平方の定理2 比の利用




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集
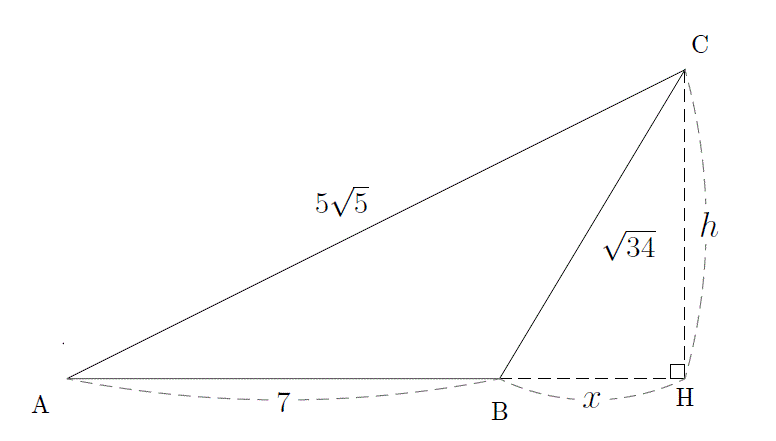



かみのドリル 三平方の定理



見本pdf 新中学問題集 発展編 塾用教材 教育開発出版株式会社 Scm H S3 Mihon




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月



直角三角形の定義とさまざまな公式 高校数学の美しい物語




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく




三平方の定理を英語で読んでみる




三平方の定理 特別な直角三角形の3辺の比 中学数学 定期テスト対策サイト



三角形の内角30度 60度 90度のとき辺の比は1 2 Root3になる Yahoo 知恵袋




数学 中3 61 三平方の定理 基本編 Youtube




三角形の各辺が3 4 5のとき直角三角形である理由 図付き なぜか分かる はかせちゃんの怪しい研究室




三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学



コラム 数学者的思考回路 13 ピタゴラスの定理 証明コレクション




交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




大工の算数 ピタゴラスの定理 小屋をつくった16年暮らした




三平方の定理の証明と使い方



Mathematics 三平方の定理 2 特別な直角三角形 働きアリ



感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




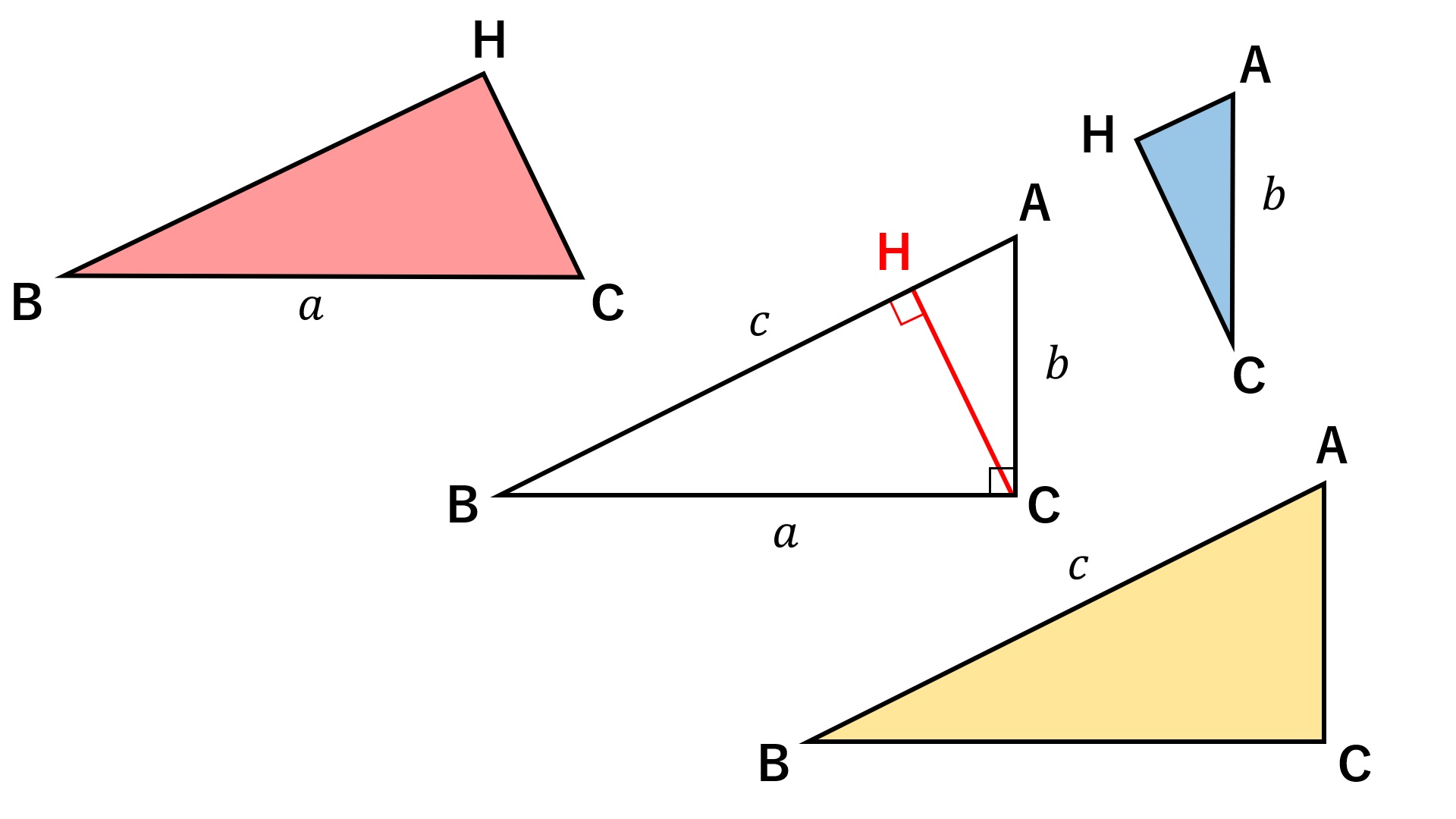
三平方の定理について考える4 三角形の相似を使った証明方法 身勝手な主張




三平方の定理 自動計算サイト




直角三角形 の画像 写真素材 ベクター画像 イメージマート




直角三角形 Wikipedia




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




三平方の定理 特別な直角三角形 イ弋マ本ゼミナール




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ
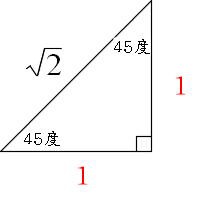



Mathematics 三平方の定理 2 特別な直角三角形 働きアリ
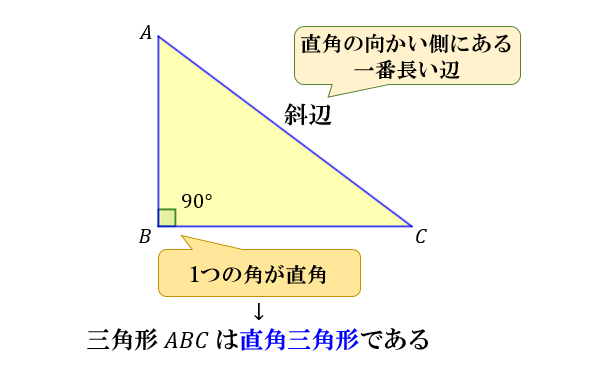



直角三角形の辺の長さ 合同条件 面積について アタリマエ




三平方の定理 無料で使える中学学習プリント




三平方の定理 ピタゴラスの定理




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット
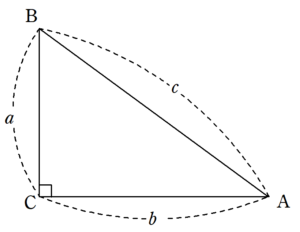



三平方の定理の証明 ユークリッドの証明 Fukusukeの数学めも




コラム ピタゴラスの定理 江戸の数学
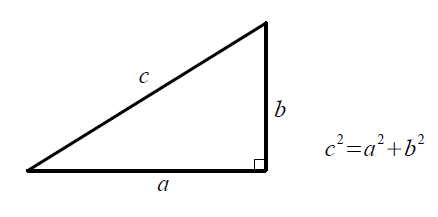



ピタゴラスの定理 ゆるゆるプログラミング




三平方の定理の応用




三平方の定理 覚えること 三角定規 苦手な数学を簡単に




中学数学 三平方の定理 30 60 90 の直角三角形 オンライン無料塾 ターンナップ




三平方の定理およびその逆 証明 理数系無料オンライン学習 Kori




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者
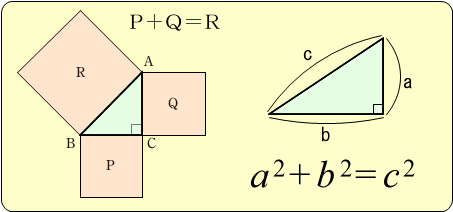



見えますか タイルの模様からピタゴラスの定理 Note Board



ピタゴラスの定理の簡単な証明方法ありますか Quora



Q Tbn And9gcq7h6dlzvq5e0plulfvxu64dpvadasyky0sizoi2drjv Uyz1m5 Usqp Cau



三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者
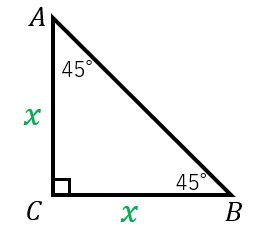



30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学




三平方の定理の逆ってなに どうやって証明するの 数スタ




三平方の定理の証明と使い方




カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 1 4



1



Http Www Edu Tens Net Kyouikuken Basic Takamatsu Pdf Jsananswer S9 07ans Pdf




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



直角三角形ではない場合ピタゴラスの定理はどう使えるのでしょうか Quora




三平方の定理 覚えておきたい基本公式を解説 数スタ



6 改めてサンキュー 直角三角形 オトナのための中学数学 天狼院書店




Junior High数学的 中学数学 三平方の定理のキホン 筆記 Clear




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



1




三平方の定理の証明と使い方




Mathematics 三平方の定理 2 特別な直角三角形 働きアリ




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




三平方の定理の証明 相似を利用した証明1 Fukusukeの数学めも



質問にお答えします 小学生でもわかる数学とは 教育研究所arcs




三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学



0 件のコメント:
コメントを投稿